Adversarial Attacks and Training Deep Learning Models

Introduction

Adversarial examples deceive machine learning models with subtle modifications. Adversarial training bolsters models by incorporating these deceptive inputs. I employed a CNN model to classify the MNIST dataset’s handwritten digits, testing FGSM attacks. FGSM attacks were most effective with epsilon values between 0.2 and 0.4.

When implementing FGSM attacks, tuning the epsilon value is crucial for achieving maximum disruption without making changes obviously visible.

Adversarial training with FGSM improved model robustness; retrained models outperformed those trained on a combined dataset of benign and adversarial examples.

Adversarial Examples

Baseline Model

The baseline model is a Convolutional Neural Network (CNN) designed to classify handwritten digits using the MNIST dataset.

The MNIST dataset is a large database of handwritten digits commonly used for training various image processing systems.

It consists of three convolutional layers, three max-pooling layers, and three fully connected layers. With the MNIST testing dataset, this model achieved 99% accuracy. This project employed the model for both adversarial attack testing and adversarial training.

Hyperparameters	Baseline Models
Input Units	1 x 28 x 28
Layers	[3 Conv2D, 3 Pool, 3 FC]
Kernel Size	[2 x 2, 1 x 1]
# of Kernels	[32, 64, 128]
Pool Size	2 x 2
Batch Size	128
Loss Function	Cross Entropy Loss
Optimization Function	Adam
Activation Function	ReLU
Batch Normalization	[128, 64]
Learning Rate	0.001
Dropout Layers	0.5
Epochs	⩾ 50

FGSM Attack

The Fast Gradient Sign Method (FGSM) Attack, introduced by Goodfellow et al., is an adversarial attack technique primarily aimed at generating visually imperceptible adversarial examples that trick image classifiers into misclassifying the images.

FGSM attacks can significantly degrade the performance of models not prepared for adversarial inputs.

The method involves the following four steps:

• Compute the gradient of the loss function concerning the input image.
• Calculate the perturbation by taking the sign of the gradient and multiplying it by a small constant (epsilon).
• Generate the adversarial example by adding the perturbation to the original image.
• Feed the adversarial example into the targeted model to induce misclassification of the perturbed image.

I adapted the attack from PyTorch FGSM Tutorial and perturbed the test images using epsilon values of 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9. These perturbed images were then subject to misclassification as part of the FGSM attack. Although the baseline model was trained in batches of 128 image samples, I modified the test loader to handle individual images perturbed through the FGSM attack to induce misclassification.

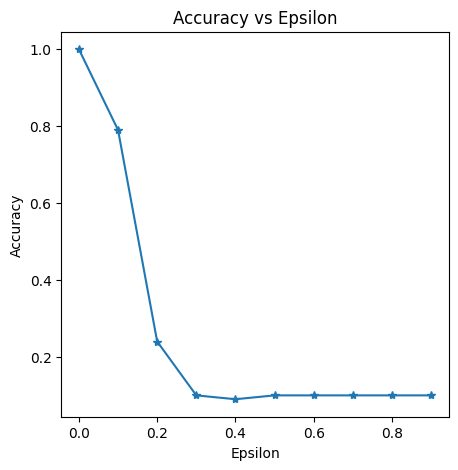Accuracy over epochs for FGSM attack on the Baseline model

I observed that as the epsilon value increases, the accuracy of the image classifier declines until it reaches a certain point, beyond which the accuracy remains unchanged. An epsilon value of 0.2 has the most significant impact on the accuracy of the image classifier, reducing its accuracy from 79% to 24%. Beyond an epsilon value of 0.4, the model no longer experiences additional accuracy loss and maintains a consistent accuracy of 10%. As a result, the most effective epsilon values for this attack on the baseline model lie between 0.2 and 0.4; increasing the epsilon value further does not impact the accuracy of the baseline model.

10 Images showcasing the FGSM Adversarial Attack on the Baseline Model

The figure above displays ten image samples from class ‘5’ of the MNIST dataset and the perturbations introduced by the FGSM attack. As the epsilon value increased, the image’s perturbation level intensified. An intriguing observation was that initially when the epsilon value was 0.2, the image was misclassified as belonging to class ‘2’. Subsequently, any increase in the epsilon value resulted in the image being misclassified as class ‘8’.

Adversarial Training

Adversarial training is a powerful defense against adversarial attacks. An iterative attack is a widely adopted technique for adversarial training, which employs multiple attack iterations to generate adversarial examples. The goal of adversarial training is to enhance a neural network model’s resilience against adversarial examples by training it with these examples. The stronger the adversarial examples used for training, the more robust the model becomes.

I train the baseline model using FGSM by iterating through several epsilon values.

Combining datasets of adversarial and benign examples can inadvertently introduce biases that affect model performance.

Adversarial Training with FGSM

The adversarial training with FGSM proceeds through the following steps:

• Generating Adversarial Examples: Adversarial examples comprising perturbed images with epsilon values of 0.05, 0.1, 0.2, 0.25, and 0.3 are generated for the 60k training samples within the MNIST dataset.
• Combining the Datasets: The generated adversarial examples are combined with the original training samples to create a new ‘combined’ training dataset of 360k images.
• Training the Model: The CNN model is subsequently trained on the combined training dataset.

I tested two FGSM adversarial training techniques:

• Retraining the baseline model with the combined dataset (Retrained)
• Train a new model on the combined dataset (Untrained).

Changing the architecture by adding additional layers or modifying the hyperparameters has been shown to affect the accuracy of the adversarially trained model. Therefore, to ensure that any changes in the model’s accuracy are solely dependent on the model’s training, I do not change the model’s architecture or hyperparameters throughout this project.

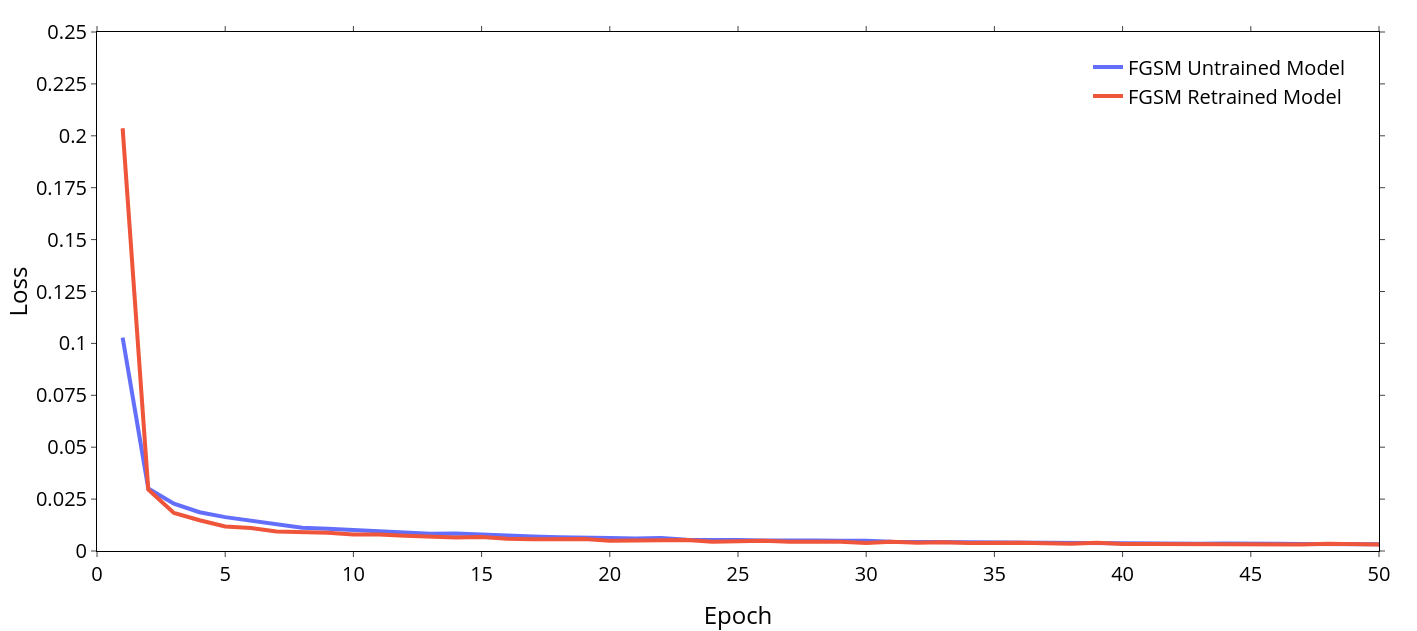Loss vs Epoch for the Original FGSM Trained (Retrained) and the New FGSM Trained (Untrained) Models

The figure above displays the training loss over epochs for both the original model retrained using the combined dataset and the new model trained on the combined dataset without prior knowledge. The untrained model’s loss began at 0.102 for the first epoch and dropped to 0.002 by the fiftieth epoch. In contrast, the retrained model’s loss started at 0.203 for the first epoch and decreased to 0.002 by the fiftieth epoch. This difference occurs because the new model learns about the dataset without prior information and can start with a lower loss than the original model. In contrast, the original model must relearn its classifications, resulting in almost double the initial loss. However, both models eventually reach the same loss over the fifty epochs, demonstrating their convergence.

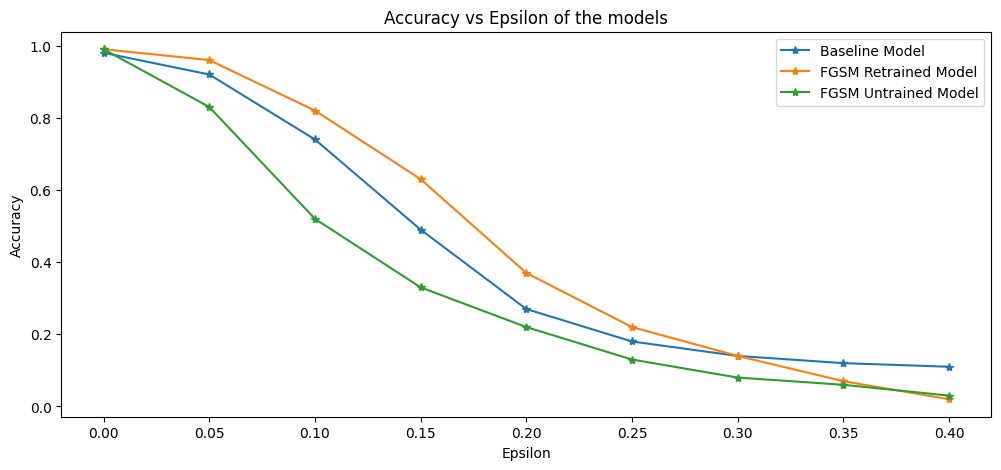Accuracy vs Epsilon for Baseline, Original FGSM Trained (Retrained) and New FGSM Trained (Untrained) Models

The figure above displays the accuracy versus epsilon of three models: the baseline model, the original model trained using the combined dataset (retrained), and the new model trained on the combined dataset (untrained). We can see that the retrained model performed better than the baseline model, while the untrained model performed the worst. At approximately 0.30 epsilon, the accuracy of the Baseline and the retrained model converged, while around 0.37 epsilon, the retrained and untrained models converged. Following this, we will use the retrained model as the default FGSM adversarially trained model. This model achieved a 98% accuracy on the non-perturbed MNIST testing dataset.

Generalization of Adversarially Trained Model

I conducted a test to check the generalization ability of adversarially trained models. I had access to two types of models – PGD adversarially trained and FGSM adversarially trained. I tested both models against FGSM and PGD adversarial attacks.

The PGD attack is a first-order attack against deep learning models. It works by computing the gradient of the loss function of the input data and then updating the input data in the gradient direction until the model misclassifies the data. Unlike the FGSM attack, the PGD attack iterates the gradient calculation process multiple times, taking small steps to generate adversarial samples with perturbations that maximize the model’s loss function. Therefore, a PGD-trained model can give us more insights into how adversarial attacks behave.

Generating adversarial datasets using PGD is the same as that used for FGSM. For each epsilon value of [0.05, 0.1, 0.2, 0.25, 0.3], 60k adversarial samples were generated, along with 60k benign training samples used to train the baseline model, resulting in a total of 360k samples. These samples were used to train two models, one by retraining the baseline model that was trained using only benign samples and the other by training a completely new model. The hyperparameters used for both training processes were the same as the baseline model.

FGSM Adversarially Trained Model

* \caption{FGSM Adversarially Trained Model against PGD Adversarial Attack*

The figure above displays the results of the PGD attack against the FGSM adversarially trained model compared to the baseline model. As expected, the PGD-trained model had the highest robustness against the PGD attack. Moreover, the FGSM-trained model also showed a high level of robustness against the PGD attack compared to the baseline model. However, when the value of epsilon was increased, the accuracy performance of the FGSM-trained model eventually dropped.

PGD Adversarially Trained Model

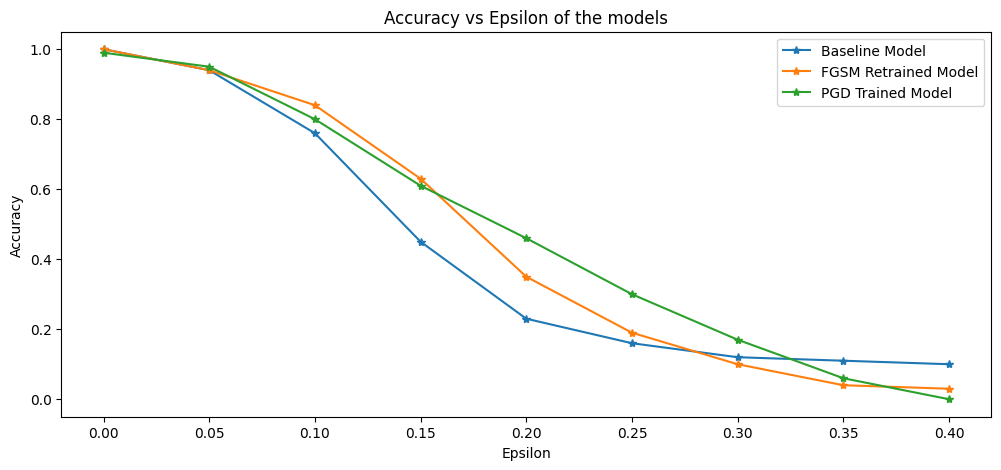PGD Adversarially Trained Model against FGSM Adversarial Attack

The figure above shows the results of the FGSM adversarial attack on three models: the baseline model, the FGSM-trained model, and the PGD-trained model. We can see increased robustness from the baseline model in the PGD-trained model up to 0.33 epsilon, after which the baseline model showed better results than the adversarially trained models. The PGD model accuracy surpassed the FGSM-trained model by around 0.15 epsilon, after which it generally provided higher robustness than the FGSM model.

Comparison

10 Images showcasing the FGSM Adversarial Attack on the Baseline 10 Images showcasing the FGSM Adversarial Attack on the PGD Trained Model 10 Images showcasing the FGSM Adversarial Attack on the FGSM Retrained Model

The figures above show ten perturbed image samples and their classifications by the Baseline, FGSM-trained, and PGD-trained models. We can see that the baseline model accurately predicted the class up to epsilon 0.15, the FGSM-trained model accurately predicted the class up to epsilon 0.2, and the PGD-trained model accurately predicted the class up to epsilon 0.25.

Analysis

Based on the results from the adversarial attack and training on the baseline CNN model, I can draw several conclusions about the relationship between attack parameters, adversarial training, and the generalization of trained models.

Adversarial Examples

I have found that the maximum range of perturbation, epsilon, is crucial in determining the effectiveness of FGSM adversarial attacks.

Understanding the relationship between epsilon and model accuracy can guide better security practices in model deployment.

The relationship between epsilon and model accuracy is not linear - there is a plateau that decreases accuracy after a specific epsilon value. This combination allows attackers to discover the optimized perturbation that maximizes the model loss.

One interesting observation is that when using FGSM on the Baseline model, all perturbed images were misclassified to a single class. This supports Goodfellow et al.’s argument about the role of excessive linearity in the model.

Adversarial Training

I noticed that the accuracy of FGSM models decreased slightly when predicting non-perturbed images compared to the baseline model. This observation confirms the robustness-accuracy trade-off discussed in the literature. It is worth noting that the FGSM Retrained model performed better than both the untrained and Baseline models. This improvement may be attributed to the retention of features from the benign dataset and the fine-tuning of the training model on the combined dataset, which allowed for better generalization and robustness.

Generalization of Adversarially Trained Models

Adversarial training enhances a model’s robustness against FGSM attacks by using the transferability property of adversarial examples. In both attack scenarios, the FGSM-retrained model showed better resistance to the PGD-trained model, possibly due to a similar diversity of adversarial examples, hyperparameter choice, or the learning of robust features during training.

However, the increase in accuracy against FGSM for the PGD adversarially trained model was lower than expected when compared to the Baseline and FGSM-trained model. This discrepancy could be due to the intentional decrease in the PGD model’s performance, label leaking, overfitting, or the model’s capacity influencing the robustness of adversarial training. Despite this, the PGD model still resisted FGSM transfer attacks. Interestingly, FGSM attacks with an epsilon value of 0.20 to 0.35 outperformed the retrained FGSM model, which is generally considered the more robust model against FGSM attacks.

Generalization of adversarially trained models may not uniformly extend to all types of adversarial attacks, indicating a need for comprehensive testing across various attack methods.

Acknowledgement

This project was a joint effort with my skilled colleague, Zhi Liu. Together, we developed implementations of FGSM and PDG, and shared the dataset and baseline models part of our assignment for the CSEC-720 Deep Learning Security course at RIT.

You can access the project by clicking here and my code files by clicking here

References

• Goodfellow et al. - Explaining and Harnessing Adversarial Examples
• Kaufman et al. - Leakage in data mining: Formulation, detection, and avoidance
• Kurakin et al. - Adversarial Machine Learning at Scale
• Madry et al. - Towards Deep Learning Models Resistant to Adversarial Attacks
• Raghunathan et al. - Understanding and Mitigating the Tradeoff Between Robustness and Accuracy
• Szegedy et al. - Intriguing properties of neural networks
• Tram`er et al. - Ensemble Adversarial Training: Attacks and Defenses
• Tsipras et al. - Robustness May Be at Odds with Accuracy